Динамическая теория приливов

Следующим после статической теории Ньютона принципиально важным шагом в объяснении механизма приливных явлений было введение Лапласом в 70-х гг. XVIII в. представления о приливных волнах. Лаплас исходил из того, что вследствие инерции воды приливный эллипсоид не может занимать положение статического равновесия.
Это несоответствие объясняется динамической теорией приливов Лапласа. Она рассматривает прилив как результат совокупного действия свободных приливных волн, приходящих из других районов, и вынужденной волны, образовавшейся в данном месте. Лаплас, так же как Ньютон, развивал теорию приливов для океана, равномерно покрывающего Землю. Он впервые получил уравнение движения приливов в океане постоянной глубины с учетом приливных сил как внешней силы. Эти уравнения позволили объяснить некоторые особенности приливов, и, в том числе, происхождение фазовых и тропических неравенств. Важный вывод, полученный Лапласом, состоял в том, что им было показано решающее значение влияния характера рельефа дна на приливы.
Статический приливный эллипсоид на вращающейся Земле можно рассматривать вне полярных областей как два возвышения и два понижения уровня, постоянно бегущих в направлении навстречу вращению Земли. Таким образом, приливы в каждой точке Земли можно представить как результат прохождения приливных волн. Длина такой приливной волны на экваторе должна равняться половине длины экватора, т. е. около 20 тыс. км. Очевидно, что такая волна является длинной практически при любой реальной глубине океана и при своем движении испытывает влияние дна.
Рассмотрим, как должны были бы распространяться приливные волны в океане. Для упрощения механизма представим, что по параллелям Землю опоясывают каналы равномерной глу

бины. В соответствии со статической теорией, Луна образует в каждом канале два возвышения уровня, в зените и надире, которые будут постоянно следовать за ее движением. Распространение этих возвышений мы можем рассматривать как вынужденные приливные волны. В отличие от них, свободными волнами, как уже отмечалось, называют такие, которые создаются кратковременным действием силы и в дальнейшем распространяются по инерции, например волны цунами.
Если бы приливные волны были только вынужденными, их движение мало отличалось бы от перемещения статического эллипсоида прилива. Но они обладают также некоторыми свойствами свободных волн, что создает ряд особенностей приливных явлений.
Скорость вынужденной приливной волны определяется тем, что она должна за сутки пройти всю длину параллели данной широты.
Длина параллели на широте ф равна              где R - ра
диус Земли. Следовательно, скорость вынужденной волны должна быть равна
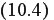(10.1)
где At- число секунд в лунных сутках.
Скорость свободной длинной волны зависит, как было показано в предыдущей главе, от глубины океана:
(10.2)
Из этих формул получаем, что для того чтобы скорости вынужденной и свободной волн на данной параллели совпадали, глубина океана должна удовлетворять условию
(10.3)
На рис. 10.7 для различных широт приведены глубины, при которых скорости распространения свободных и вынужденных приливных волн совпадают.


Рис.

10.7. Глубины на различных широтах, при которых скорости распространения свободных и вынужденных приливных волн совпадают


Из рис. 10.7 видно, что для совпадения скоростей свободных и вынужденных приливных волн в значительном диапазоне широт необходимы чрезмерно большие глубины каналов, превышающие фактические глубины на этих широтах. При глубинах каналов, сравнимых с реальными глубинами океана, приливные волны в низких широтах должны иметь тенденцию отставать от светила. Отсюда получает объяснение возникновение прикладного часа. На экваторе, как показывает теория, прилив должен быть даже «обращенным», т. е. в моменты кульминации светила должны наблюдаться малые, а не полные воды. В высоких широтах приливные волны могут не отставать от светила и даже должны иметь тенденцию опережать его и распространяться как свободные волны.
В канале, расположенной на некоторой широте, сочетание длины параллели и глубины может оказаться таким, что время обегания свободной и вынужденной волн будут равны, и амплитуда прилива сильно возрастет. В реальном океане условия, в некоторой степени подобные каналу, вытянутому по параллели, существуют в Южном океане, опоясывающем антарктическую область. Поэтому были высказаны гипотезы о том, что в этой области генерируются прогрессивные приливные волны, распространяющиеся с востока на запад и благодаря рефракции заворачивающие к северу в другие океаны.
За распространением приливных волн можно наглядно проследить по наблюдаемым моментам наступления полных вод на береговых и островных пунктах. Отсчитывая эти моменты от какого-либо определенного начала счета времени, например, от момента кульминации Луны на гринвичском меридиане, можно построить карту ежечасных положений изолиний полных вод - котидальных линий. На рис. 10.8 изображены котидальные линии полусуточного лунного прилива, вносящего, как мы знаем, основной вклад в наблюдающиеся приливы.

Рис. 10.8. Котидальные линии и линии равных величин приливов для главной лунной составляющей волны М2 в северной части Атлантического океана:
1 - средняя поправка времени полных вод (в ч) относительно прохождения Луны через Гринвичский меридиан;
2 - составляющая приливной волны М2 (в дм)



Как видим, только в отдельных районах океана приливные волны распространяются, как обычные поступательные волны. В большинстве районов перемещение приливных волн оказывается довольно сложным. Это связано с тем, что в каждом океане возникают и собственные приливы, имеющие часто характер стоячих волн. Происходит интерференция прогрессивных и стоячих волн, отражение волн от берегов.
Котидальные линии обращаются вокруг центра бассейна, в котором нет колебаний уровня - амфидромической точки. На котидальной карте (см. рис. 10.8) имеется несколько амфидро- мических областей. Они указывают на то, что в этих районах океана значительный вклад в приливные явления вносят стоячие приливные волны.
Полная расчетная формула Лапласа с поправочными коэффициентами, дающая неплохие результаты только для предвычисления правильных полусуточных приливов, не получила практического применения. Однако предложенный Лапласом принцип решения задачи положен в основу метода гармонического анализа. 

Еще по теме Динамическая теория приливов:

1. Приливы, литораль
2. Разнообразие динамических процессов в популяциях растений разных жизненных форм
3. Суточные изменения оборонительно-пищевого поведения животных в связи с явлением приливов и отливов
4. ОПЫТ количественной оценки динамических СОСТОЯНИЙ И УСТОЙЧИВОСТИ СОСНОВЫХ НАСАЖДЕНИЙ НАОБЪЕКТАХ ГИДРОМЕЛИОРАЦИИ
5. Гормональная теория
6. ТЕОРИЯ, ЭВОЛЮЦИЯ И ТЕОРИЯ ЭВОЛЮЦИИ
7. 2.1. КЛЕТОЧНАЯ ТЕОРИЯ
8. Теория филэмбриогенеза
9. Мозаичная теория развития
10. 1. Какая нужна теория?
11. Теломная теория
12. Теория параллелизм
13. Глава 17. ЭВОЛЮЦИОННАЯ ТЕОРИЯ
14. Теория Тэта — MEST
15. Теория типов в эмбриологии
16. ТЕОРИЯ АГРЕГАЦИИ ПОЧВ
17. Популяции и синтетическая теория эволюции
18. Теория вида у высших растений