Простые модели размножения

Возраст семьи, дни
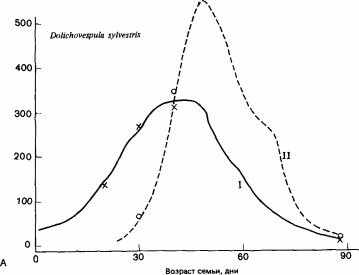
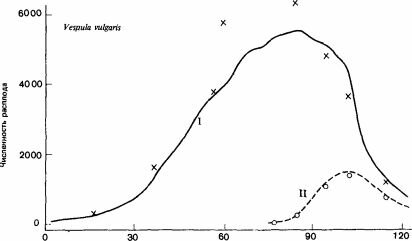
Рис.

11.1. Теоретические кривые динамики развития семей Dolichovespula sylvestris и Vespula vulgaris, рассчитанные на ЭВМ.
Показана зависимость числа личинок в мелких (I) и крупных (II) ячейках от возраста семьи. (Archer, 1981а.)
Простейшие модели строятся с учетом взрослых особей только двух категорий- рабочих и половых особей; количество яиц и снабжение кормом предполагаются достаточными. В одной модели число рабочих, имеющихся в данном интервале времени, есть экспоненциальная функция от их числа в предыдущем интервале (при показателе степени меньше 1), а образование молодых самок пропорционально числу рабочих (Brian, 1965). В такой семье возможно образование столь большого числа половых особей, что они уничтожат или по крайней мере сильно подорвут ее возможности в смысле производства рабочих особей, или-другая крайность - половых особей может возникать так мало, что продуктивность сообщества окажется пониженной, если измерять ее как соотношение репродуктивные самки/рабочие особи. Между этими крайними состояниями неустойчивости и неподвижности существует состояние, приближающееся к равновесию в режиме затухающих колебаний. В этом случае, конечно, есть опасность того, что случайные отклонения могут привести к вымиранию, так что продукция благополучного многолетнего сообщества окажется ниже, а не выше нормы. Вместе с тем семья может выдерживать ежегодное вымирание благодаря тому, что специально подготовленные плодовитые самки переживают зиму, как, например, у Vespula или Bombus, и это дает возможность семье достигать высоких скоростей продукции половых особей и
высокой продуктивности на одну рабочую особь в летнее время. Такой результат возможен при полном переключении с производства рабочих особей на продуцирование половых особей, однако в этом случае чрезвычайно важны сроки. Если такое переключение произойдет слишком поздно, то не останется времени для копуляции и подготовки к зиме, а если слишком рано, то будут напрасно потеряны продуктивные летние дни; таким образом, проблема опять-таки заключается в том, чтобы согласовать цикл развития семьи со сменой времен года.
Lovgren (1958) смоделировал это для ос. Archer (1981а), составивший обзор различных моделей и построивший модели годичных циклов двух европейских представителей Vespidae, обнаружил различия в том, каким образом производство половых особей связано у них со временем года (рис. 11.1). У Dolichovespula sylvestris первые крупные ячейки для репродуктивных самок и самцов строятся в тот период, когда скорость строительства мелких ячеек для рабочих максимальна, а возраст семьи всего лишь 30 дней. Это соответствует теории максимизации производства половых особей. В отличие от этого Vespula vulgaris начинает постройку крупных ячеек, когда скорость создания мелких ячеек начинает снижаться (на 7-8 недель позднее, чем D. sylvestris), и таким образом создает гораздо большее число рабочих особей. В то время как D. sylvestris целиком переключается с производства рабочих на выведение половых особей, V. vulgaris, начав строить крупные ячейки, некоторое время продолжает строить и мелкие. Это не так странно, как кажется, потому что у этого вида значительная часть самцов развивается в мелких ячейках и их продолжающуюся постройку можно рассматривать как часть программы создания половых особей. Поскольку у V. vulgaris это длится дольше, у нее в конечном итоге получается больше молодых самок на одну матку, но рабочие используются гораздо менее эффективно: если говорить о соотношении молодых самок и рабочих, то у V. vulgaris оно равно 0,18, а у D.sylvestris-!,66. Более обширное гнездо V. vulgaris позволяет поддерживать достаточно высокую температуру поздним летом и делает возможным более быстрое развитие, что опять-таки снижает расходы на создание одной репродуктивной особи. Таким образом, благодаря более продолжительному сезону размножения и выведению репродуктивных особей в конце сентября, а не в конце июля у V.

vulgaris продукция молодых самок выше, хотя они используют своих рабочих менее эффективно. Быть может, этот вид мог бы существововать и в более теплом климате, где ему не надо было бы готовиться к зимовке? Spradbery (1973b) нашел, что V.germanica-близкая родственница V. vulgaris, интродуцированная на Тасманию,-действительно способна к этому. С другой стороны, вид D. sylvestris, несомненно, вполне мог бы обитать в местах с более коротким летом; Archer перечисляет 20 признаков, по которым D. sylvestris отличается от V. vulgaris и которые, по-видимому, делают его более приспособленным к жизни в областях с коротким летом, в более высоких широтах и на большей высоте, чем V. vulgaris.
Модель, пригодную для многолетних сообществ любых видов (например, Myrmica), которые собирают корм и откладывают яйца в зависимости от его количества, разработали Brian et al. (1981а) и в еще более общем виде Frogner


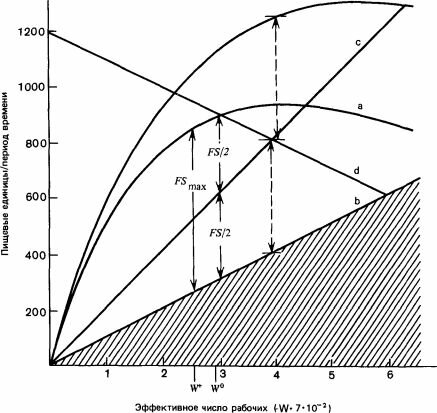
Рис. 11.2. Модель семьи Myrmica. В этой численной модели семьи с одной самкой скорость сбора корма зависит от числа рабочих особей (кривая а). Прямая 6-количество корма, необходимого для поддержания численности рабочих особей на постоянном уровне. Поэтому а — b соответствует количеству корма, который может быть использован для производства репродуктивных особей. Оно достигает максимума при W = Wv. Это, однако, не соответствует тому количеству корма, который обеспечивает генетически оптимальный вклад в производство таких особей (см. гл. 2); наименьшая численность
семьи, при которой этот избыток делится поровну между двумя полами, равна Ш1, и Wlt;gt;gt; W +. Если семья находится в наилучшем для нее местообитании с источником корма соответствующей плотности, го отношение собираемого корма к численности рабочих особей будет описываться кривой е, а прямые end будут соответствовать распределению этого избытка между самцами (с) и самками (id). Точка пересечения с и o'соответствует случаю, когда вклад в самцов и в самок одинаков; при этом W — 400, т. е. все еще выше IE0, которое соответствует состоянию, когда семья получает достаточное количество корма. (Brian et al., 1981а.)

(1980). В первой модели рассматривается семья, начало которой кладут самка, несколько рабочих особей и расплод, выращиваемый за счет запасов, содержащихся в мышцах и жировом теле самки. Для новых рабочих особей характерна определенная продолжительность жизни, они способны собирать и перерабатывать корм, но по мере роста их числа они становятся менее эффективными из-за перенаселенности; поэтому с увеличением общей численности семьи количество собранной пищи в пересчете на одну рабочую особь возрастает гораздо медленнее. Модель исходит из того, что потребность в энергетическом материале, пропорциональная числу рабочих, приводит к максимуму сбора корма раньше, чем начинает сказываться потребность большой армии рабочих в энергии. Этот максимум все еще значительно больше того количества пищи, которое необходимо для замещения гибнущих рабочих особей, и ее избыток используется для выращивания половых особей (рис. 11.2); если же последнее из модели исключить, то этот избыток будет расти до тех пор, пока самка не прекратит откладку яиц или пока из-за помех, связанных с излишком рабочих особей, сбор корма не снизится настолько, что его будет едва хватать на замещение гибнущих рабочих. Достижению такого равновесия предшествует фаза затухающих колебаний, обусловленных тем, что между откладкой яйца и появлением рабочей особи должно пройти некоторое время (период развития) (Maynard Smith,

1974. , и поэтому число рабочих, определяющее темп откладки яиц в каждый данный момент, не равно тому их числу, к которому позднее добавятся новые особи, развившиеся из этих яиц.

В главе 12 будет описана модель продуктивности Myrmica limanica,
в которой учитывается различие во вкладах особей разного пола (Uchmanski, Petal, 1982).

Еще по теме Простые модели размножения:

1. 5-10. Экспериментальная эволюция. Модели размножения
2. Математические модели в экологии. Модели биогеоценозов
3. Эфирная модель строения атома
4. Модели роста популяций. 
5. Анализ моделей и сценариев
6. 19.1. ТИП ПРОСТЕЙШИЕ PROTOZOA
7. Общая характеристика простейших
8. Простейшие
9. Простейшие
10. Модели межклеточного взаимодействия и формообразования
11. 3. Познавательные модели эволюционизма
12. Модели изложенных теорий
13. 3.3. Модель строения атомного ядра
14. 1-11. Человек - модель эволюции
15. ТИП ПРОСТЕЙШИ
16. ПРОСТО ОБЕЗЬЯНЫ
17. 19.3. Простейшие, обитающие в тканях
18. ПАРАМЕТРИЗАЦИЯ БОЛОТВ МОДЕЛИ ЧИСЛЕННОГО ПРОГНОЗА ПОГОДЫ ПЛАВ А. Ю. Юрова, М. А. Толстых
19. 19.2.3. Простейшие, обитающие в толстой кишке
20. 19.2.2. Простейшие, обитающие в тонкой кишке