Взаимодействия насекомого-фитофага и растения

В случае повреждения насекомыми растение способно "мобилизовать" защитные реакции и повысить свой иммунитет. При этом растение изменяет определенным образом свой химический состав, и начинает отпугивать насекомых.

Однако при массовом размножении фитофага растение ослабляется и становится неспособным противостоять нападению. В этом случае возникает положительная обратная связь, приводящая в конце концов к распаду системы, т. е. к гибели растения. Интересный пример таких взаимодействий приводят А.С.Исаев и др. (1984), описывая динамику взаимодействия большого хвойного черного усача (Monochamus urussovi Fisch.) с его кормовым деревом - сибирской пихтой. Личинки этих жуков питаются лубом и частично древесиной, пихта же отлично защищается от них, интенсивно выделяя смолу. Но только здоровые деревья способны противостоять нападению усача. Поэтому жуки развиваются в основном за счет ветровала и отдельных старых и ослабленных деревьев, не причиняя вреда лесу. В какой-то мере жуки могут быть даже полезными, устраняя отстающие в росте деревья. Имаго же питаются, объедая кору с веток и иногда даже их окольцовывая. В норме этих жуков немного и они не наносят деревьям существенного вреда. Такая устойчивая популяция усача может существовать сколь угодно долго.

Совсем иная ситуация возникает при ослаблении и гибели части деревьев под влиянием пожаров, промышленных выбросов или после массового размножения сибирского шелкопряда, объедающего всю хвою. В этом случае жуки исходно имеют много субстрата, пригодного для развития личинок. Жуки размножаются в массе, и повреждений, наносимых имаго, становится так много, что от них ослабляются и практически здоровые деревья.

Численность популяции резко возрастает, и вспышка кончается только после гибели всех пихт в лесу.

В экологической литературе хищникам и особенно паразитам уделяется большое внимание, так как предполагается, что именно они регулируют численность популяции, увеличивая свой пресс при массовом размножении их жертв и ослабляя его в годы с низкой численностью.

Здесь мы основное внимание уделим паразитам, как влияющему на численность фактору. Модели хищничества очень близки к моделям паразитизма. Основное различие заключается в том, что у паразита число отложенных им яиц определенным образом соответствует числу найденных им хозяев, у хищника же эта связь не столь однозначна.

Простейшая модель взаимодействия популяций хозяина и паразита была представлена У.Томпсоном (W.R.Thompson, 1924). Эта модель была разработана для случая, когда плотность популяции хозяина исходно высока и поэтому паразит тратит мало времени на поиск. Предполагается также, что при каждой встрече самка паразита будет откладывать в хозяина по одному яйцу, (что не исключает возможность повторного заражения при последующей встрече). Тогда число отложенных всеми паразитами яиц N (=число встреч с хозяином) может быть определено по формуле:

N = PF,

где P - численность (плотность) паразита, а F - его средняя плодовитость. Если плотность определяется в расчете на 1 м 2 , то PF - это количество яиц, отложенных на 1 м 2 .

При случайном (пуассоновском) распределении яиц хозяина и возможности многократного заражения при повторных встречах, доля незараженных хозяев равна:

- PtF

Q = e ~ж, (10)

где е - основание натуральных логарифмов, Pt - плотность паразита в поколении t, Nt -

плотность популяции хозяина в поколении t, F - плодовитость паразита.

Соответственно, плотность популяции хозяина в поколении t+1 будет:

PtF

Nt+1 = Nt 1e Nt, (11)

а плотность популяции паразита в поколении t+1 будет: f PtF Л 1 - e

Nt

(12)

P = N

V+1 iNt

При такой ситуации возможны два выхода: либо продуктивность паразита окажется слишком мала, чтобы существенно снизить биотический потенциал хозяина - тогда обе популяции будут увеличивать свою численность, либо паразит уничтожит всех хозяев и вымрет сам. При введении в модель верхнего уровня численности хозяина, допускаемого ресурсами, модель предсказывает полное вымирание и хозяина, и паразита. Если ввести в формулу верхний порог численности паразита, вся система может существовать неограниченно долго. Однако модель Томпсона основана на неверной предпосылке о независимости количества яиц, отложенных паразитом, от плотности популяции хозяина. Этого недостатка лишена модель Л.Никольсона и В.Бейли (A.J.Nicholson, V.A.Bailey, 1935), которые также пытались объяснить имеющее обычно место в природе длительное сосуществование паразита и хозяина.

Эти авторы исходили из следующих предположений. В течение своей жизни самка паразита в поисках хозяина обследует определенную площадь - а. Величину этой площади можно считать в среднем постоянной и характерной для вида. Можно предположить далее, что поиск беспорядочен и траектория движения самки напоминает броуновское движение. Действительно, например, у трихограммы перемещение самок в поисках яиц хозяина происходит по сложной запутанной линии (рис.32) (отметим, однако, что при попадании на участок поверхности, загрязненной кайромоном - привлекательным для паразитов веществом, оставляемым бабочкой на поверхности при откладке яиц, характеристики движения трихограммы меняются и резко возрастает число поворотов). Другое предположение этих авторов - количество яиц, которое может отложить самка паразита, не ограничено по сравнению с числом хозяина.

Приняв эти предположения, перейдем к самой модели. Очевидно, что если плотность популяции хозяина N, а самка паразита обследует площадь а, то она встретит и соответственно заразит а N хозяев, т. е. ее плодовитость F = a N.

Рис.32. Пример траектории движения трихограммы на горизонтальной плоскости. Точки нахождения трихограммы через определенные интервалы времени соединены прямыми (по В.Б.Чернышеву и др., 1988)

P« = N,(1 - e-aPt) (13)

Если территория, обследуемая одной самкой, равна а, то группа самок P обследует площадь, меньшую произведения aP, так как траектории самок перекрещиваются друг с другом. Анализ этих случайных перекрытий обследованных территорий показывает, что имеет место следующее соотношение:

N

ln—L = aP, (14)

St

где Nt - исходное число хозяев, St - число хозяев, оставшихся незараженными. Соответственно, зная плотности популяций паразита и хозяина, а также процент зараженных хозяев, можно определить величину территории а, обследуемой одной самкой. Если каждая выжившая особь хозяина производит в среднем FN потомков (плодовитость хозяина), то плотность популяции хозяина в поколении t+1 будет равна:

Nt+1 = S,Fn .

Эту формулу можно переписать следующим образом:

S

N = N —LF

1п+1 t N

Логарифмируя это уравнение, получаем:

N

lnNt+1 = lnNt - ln—L + lnFN.

St

или, используя равенство (14):

lnNt+1 = lnNt - aP + lnFN. (15)

Пользуясь последней формулой, можно рассчитать плотность популяции хозяина в последующем поколении. Очевидно, что число паразитов в следующем поколении должно быть равно числу зараженных хозяев в предыдущем поколении.

Эта модель была проверена в теплице, где имелись белокрылки Trialeurodes vaporariorum и ее паразит Encarsia formosa (T.Burnett, 1958). Результаты этого эксперимента представлены на рис. 33. Можно видеть неплохое совпадение теоретически вычисленных и экспериментальных данных.

В принципе, вся система будет равновесной, если Nt = Nt+1 = Nt+2 и т.д. Если подставить это равенство в формулу (15) мы получаем, что: aP = ln FN

Поколения -

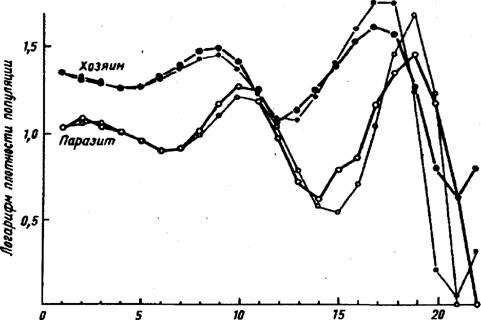
Рис.33. Взаимодействия между популяциями тепличной белокрылки Trialeurodes и ее паразита Encarsia в опытной теплице. Толстые линии - результаты наблюдений, тонкие линии - расчет по формуле (по Т.Бернету из Дж. Варли и др., 1978)

Колебания численности хозяина и паразита должны возникать и, исходя из формул, предложенных А.Лоткой (A.Lotka, 1925). Для описания роста численности хозяина была предложена следующая формула:

= rN - kNP,

dt

где r - биотический потенциал хозяина, N - его численность, P - численность паразита и k - коэффициент взаимодействия, пропорциональный числу жертв паразита.

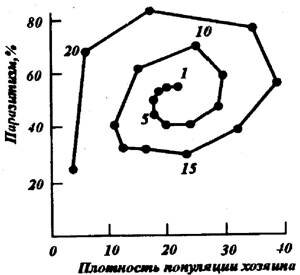
Рис.34. Данные рис.33, представленные как изменения соотношения между численностями популяций хозяина и паразита во времени. Цифры у кривой оказывают номер поколения (по Дж. Варли и др., 1978)

— = kNP - DP, dt

где D - показатель смертности паразита по разным причинам. Колебания возникают в этой модели, как и в предыдущей, потому, что рост численности хозяина увеличивает численность паразита лишь с некоторым запозданием.

На рис.35 показаны такие теоретически предсказанные колебания на примере лабораторных культур двух видов клещей: растительноядного и хищника.

Время в неделях

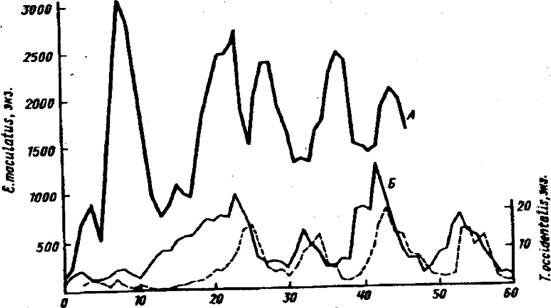
Рис.35. Колебания численности лабораторной культуры паутинного клеща Eotetranychus maculatus в чистой культуре (А) и при взаимодействии с хищным клещом Typhlodromus occidentalis (Б). Сплошная линия - жертва, пунктир - хищник (по C.Huffaker et al..ro Г. А.Викторова, 1967)

Одно из наиболее рискованных допущений модели Никольсона-Бейли, что плодовитость паразита беспредельна и количество отложенных яиц увеличивается прямо пропорционально плотности популяции хозяина, независимо от ее уровня. Чаще всего с ростом численности хозяина происходит как бы "насыщение", возможности паразита исчерпываются и доля зараженных хозяев становится все меньше. Это связано с тем, что как паразит, так и хищник должны потратить на жертву определенное время - время "обработки". С ростом численности жертвы сокращается только время поиска, но не время "обработки". Остроумная модель подобной реакции была предложена К.Холлингом (C.S.Holling, 1959). На стол случайным образом выкладывали диски из наждачной бумаги диаметром 4 см каждый. Испытуемая с завязанными глазами садилась за стол и на ощупь искала диски, а находя их, откладывала в сторону. Такой поиск продолжался в течение одной минуты. Опыты повторялись многократно, причем число дисков на столе менялось от 4 до 256 на 9 квадратных футов. Итог этих экспериментов показан на рис.36. Подобные же кривые были получены ранее в экспериментах, где паразиту предоставлялось разное количество хозяев для заражения. Начиная с определенной численности хозяина, число зараженных особей оставалось практически постоянным, например для хальциды Dahl- bominus fuscipennis (T.Burnett, 1956), заражающей куколок пилильщика Neodiprion sertifer и для других паразитов, например Mormoniella vitripennis, заражающего пупарии синантропных мух (E.S.Smirnov, M.S.Wladimirova, 1934). Интересно, что кривые на графиках, полученных Е.С.Смирновым и М.С.Владимировой, переходят в линии, параллельные оси абсцисс на разных уровнях в зависимости от вида хозяина. Следовательно, "обработка" пупария, например комнатной мухи или каллифоры, занимает разное время. Кроме того, время "обработки" жертв может увеличиваться и с насыщением хищника (H.Harvonen, E.Ranta, 1992).

Математическая модель, предложенная К. Холлингом, может быть выражена следующей формулой:

Формула

где P t+1 - плотность популяции паразита в следующем поколении, что равной числу найденных и зараженных предыдущим поколением хозяев, Т - длительность интервала времени, в течение которого проводится поиск, T h - время "обработки" (handling) хозяина, Nt - плотность популяции хозяина, с - быстрота обнаружения хозяина (скорость поиска, умноженная на вероятность его нахождения). Модель Холлинга в определенной степени 25

20

15

10

обобщает модели Томпсона и Никольсона- Бейли, которые являются ее частными случаями. Однако модель Холлинга основана на предположении о бессистемном поиске жертвы, в природе же паразита часто привлекают кормовые растения хозяина или его скопления.

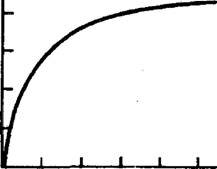
Рис.36. Количество дисков наждачной бумаги - "жертв", найденных за 1 мин наблюдателем - "хищником" на ощупь в зависимости от количества этих I дисков, положенных перед ним на столе

популяции жертвы") (из C.S.Holling по P.Price, 1984) Итак, очевидно, что как паразиты, так и хищники могут сдерживать кассовое размножение хозяина только до определенного его предела. Несдерживаемый рост численности хозяина выше этого предела называют ускользанием. Этому эффекту придают большое значение в объяснении массовых размножений насекомых.

Возможность дестабилизации естественными врагами численности хозяина является выводом практически всех моделей, описывающих эти взаимодействия (А. А. Шаров, 1986). Подчеркнем, что это не означает, что паразиты и хищники непригодны для биометода, так как обычная цель последнего не столько стабилизация численности вредителя, сколько снижение этой численности.

Эффективность подавления хозяина паразитом или хищником q - может быть определена по формуле

q = N1/N0,

где N1 - плотность популяции хозяина после выпуска искусственно заеденного паразита, a N0 - плотность популяции до выпуска. Использование биометода можно считать удачным при значении q в пределах от 1/40 до 1/300 (M.P.Hassell, D.Wange, 1984). Однако необходимо помнить, что при очень высокой численности вредителя, способствующей конкуренция за пищу и распространению заболеваний, интродуцированный паразит, устраняя часть хозяев, может ослабить внутривидовую конкуренцию таким образом, продлить массовое размножение. Правда, использование химического метода приводит в первую очередь к уничтожению паразитов и этим создает условия для новой вспышки размножения вредителя.