Моделирование континуальности и дискретности
Обитающие совместно виды взаимодействуют друг с другом. Взаимодействия эти могут быть как связанными с переносом энергии (трофическими), так и не связанными. Последние весьма разнообразны и могут быть не менее важными для популяций, чем трофические, хотя на современной стадии своего развития экология изучает прежде всего пути переноса вещества и энергии (цепи питания, конкуренция за ресурс, динамику биогенов и т.
д.). Предложено большое число классификаций взаимодействий видов по самым разным логическим основаниям или вовсе без них. Ещё больше классификаций может быть предложено. Если же начать классифицировать не только парные, но и множественные взаимодействия, число возможных классификаций возрастёт почти до бесконечности. Для дальнейшего изложения достаточно констатации факта сложности и многообразия взаимодействий отдельных видов.Существенный вопрос, который даст весомые аргументы в пользу континуализма или структурализма, следующий: достаточно ли слабых позитивных взаимодействий видов для образования устойчивых в пространстве и времени ассоциаций? Положительный ответ на этот вопрос будет означать, что для объяснения наблюдаемого распределения видов в пространстве отнюдь не всегда нужно привлекать абиотические факторы, как это делают континуалисты. Отрицательный же — наоборот, будет свидетельствовать о том, что учитывать влияние среды необходимо для объяснения случаев совпадения пространственного распределения видов. В природе трудно найти убедительные примеры, поскольку неоднородности биоты наблюдаются на фоне неоднородностей абиоты.
Но неоднородную абиотическую среду легко создать в модели. Рассмотрим другую модель (тоже клеточный автомат), которая позволит ответить на поставленный вопрос.
Представим простейшую систему:
- состоящую всего из двух пар видов A-а и В-Ь;
- совместно могут быть встречены только виды разных регистров (вид, обозначенный большой буквой с видом, обозначенным маленькой и наоборот);
Табл.
4.1. Матрица перспектив вида а.Исходное Вероятность Результат
население события
| А | 1 | Ala |
| -/- | 0,5+Ass/2 | -la |
| А/Ь | 0,5+Ass/2 | Ala |
| -1Ь | 0,5 | -la |
| В/- | 0,5-Ass/2 | B/a |
| В/Ь | 0,5-Ass/2 | B/a |
- пусть между видами A-а и В-b существует позитивная связь, а между видами А-b и В- а - негативная.
Всё многообразие взаимодействий видов формально выразим в изменении вероятности совместного обнаружения: виды, взаимодействующие позитивно, имеют повышенную вероятность совместного нахождения, взаимодействующие негативно — отрицательную. В модели этот параметр (Ass) варьирует от -1 до +1. При значении Ass = 0 связь между видами отсутствует, при Ass = -1 или 1 связь функциональна.
В каждом поколении модели каждая особь размножается (простым делением), продуцируя подобных себе потомков (число потомков задаётся). Каждая дочерняя особь расселяется в случайно выбранном направлении на случайную дистанцию (радиус расселения задаётся) и производит попытку занять выбранное место. В зависимости от населения последнего, расселяющаяся особь занимает участок или вымирает согласно следующей матрице вероятностей (как пример в табл. 4.1 рассмотрен вид а). Если место занято видом А, то особь а займёт его и разделит впоследствии с особью А. Если место пусто, то
а займёт его с вероятностью 0,5 + Ass/2. С такой же вероятностью а вытеснит Ь, если Ь занимает место совместно с А. В случае, если Ь является единственным хозяином участка, а вытеснит его с вероятностью 0,5. Если участок занят В, либо В в паре с Ь, то а становиться совладельцем участка с В с вероятностью 0,5 -
| ШИ | 1 | в | ||
| иИ | ¦ | сг | а |
Рис.
4.6. Два варианта исходных распределений видов.Ass/2. Судьба вытесненных особей для конечного результата несущественна, для простоты положено, что все вытесненные особи погибают. В каждом поколении модель сканирует особи в случайном порядке.
Распределение видов показывается в модели в окне, поделённом на две части. В верхней показано распределение видов А и В, в нижней — а и Ь.
Модель позволяет задавать два возможных начальных типа распределения (рис. 4.6). на поверхности тора (тор выбран для простоты моделирования, форма поверхности не
важна). При одном (слева) распределение случайное. При втором (справа) распределение
максимально неслучайное и антагонистичное (совместно обитающие в исходном распределении виды взаимодействуют негативно): одна часть моделируемого пространства заселена видами А и Ь, другая — В и а, заселённые участки разделены незаселённым пространством. Случай, когда совместно обитают позитивно взаимодействующие виды, не рассматривается. Впрочем, как выяснилось при прогоне модели, влияние начального распределения видов быстро становится несущественным.
На рис. 4.7 показано как меняется через 50 поколений исходно случайное (в центре) распределение в зависимости от разных значений (цифры) связи видов. Вверху показано распределение видов А и В, внизу — а и Ь. Как и следует ожидать, в отсутствии связи между видами их распределение независимо друг от друга. Распределение пар видов А-а и В-Ь независимо. Однако уже при значении параметра связи 0,1 совпадение распределения положительно взаимодействующих видов становится очевидным. Напомню, что такая сила связи свидетельствует, что лишь одна из 10 особей при занятии участка руководствуется предпочтениями в выборе партнера. Дальнейшее увеличение силы связи сначала увеличивает скорость, с которой устанавливаются резкие границы, а затем приводит к возрастанию мозаичности.
В пределе (при связи = 1) мозаичность столь высока, что производит впечатление случайного распределения. В действительности же все ячейки заняты либо Аа, либо ВЬ, но скорость, с которой образуется комплементарное распределение при изначально заданном случайном распределении, столь высока, что обширные однородные участки просто не успевают образоваться. Таким образом, результат не зависит от силы связи видов: при любой образуются участки, занятые той или иной парой видов.Булыпее число потомков и меньший радиус расселения ускоряет формирование однородных участков, меньшее число потомков и больший радиус расселения — замедляют. Т. е. эти особенности биологии влияют лишь на скорость, но не на результат: рано или поздно ассоциации, образованные положительно взаимодействующими видами, занимают сплошные области.
Образующиеся между областями границы не просто устойчивы во времени, более того, их чёткость в ряду поколений только возрастает, при этом граница становится менее извилистой (рис. 4.8).
Таким образом, для возникновения неоднородности в распределении видов совершенно не нужна неоднородность среды, достаточно лишь того, чтобы виды взаимодействовали друг с другом (влияли на распределение друг друга), т. е. происходило то, что в природе наблюдается часто и обычно. Эта неоднородность образуется в результате самоорганизации и устойчива во времени.
| • щ | |
| й | ш |
|
’ Шь
ш |
щ |
|
дат*1
К--* |
м |

Рис. 4.7. Влияние силы связи видов на их распределение.




75

100
IHL- І
Рис.
4.8. Устойчивость границ во времени.0,1
0,01



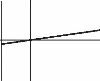
Рис. 4.9. Влияние градиента.
Вверху: зависимость резкости границы от значение градиента, внизу — изменение положения границы вслед за изменением положения нейтрального значения градиента.
Остаётся неясным, с чем же связано то, что при более или менее тщательных поисках обычно удаётся обнаружить, что границы неоднородности биоты часто соответствуют тем или иным неоднородностям среды. Для этого введём в модель неоднородность среды в простейшем виде — как градиент фактора среды, причём при значениях фактора gt;1 одна из пар имеет конкурентное преимущество, lt;1 — другая, а при = 0 ни одна, ни другая пара не имеют конкурентного преимущества. При значениях фактора = 0,01 конкурентное преимущество реализуется в 1 случае из 100 при максимальном значении фактора. На графике (рис. 4.9) это выражено в угле наклона линии фактора: при 0 она параллельна оси X (градиент отсутствует), при 1 — перпендикулярна ей. Сразу же становится очевидным, что даже незначительный градиент существенно влияет на распределение комплексов видов: граница между комплексами становится перпендикулярной градиенту среды. При смещении равновесного положения в ту или иную сторону, граница между комплексами движется вслед за ним. Стоит отметить также, что даже при плавном градиенте граница между комплексами весьма резка, совпадая со значением фактора = 0, при котором обе пары имеют одинаковые конкурентные возможности (на графике соответствует оси X).
«Ежели у тебя спрошено будет: что полезнее солнце или месяц, ответствуй: месяц, ибо солнце светит днём, когда и без того светло» (Козьма Прутков.
Плоды раздумья. Мысли и афоризмы. 51).Таким образом, хотя градиент среды не является необходимым для возникновения границы между комплексами видов, положение границы зависит от градиента: равновесное значение (при котором конкурентоспособность пар равна) является аттрактором. Поскольку абсолютно однородная среда возможна только в компьютерной модели, но не в природе, соответствие градиентов среды границам между комплексами видов должно быть весьма обычным. При рассмотрении работ, в которых показывают возможность объяснить распределение видов факторами внешней среды, следует помнить, что любой самый совершенный математический аппарат ищет связи только среди переменных, которые введены в анализ. Первым же этапом любого анализа является ограничение набора рассматриваемых переменных теми, которые исследователь считает значимыми. Поэтому дальнейший анализ устанавливает только то, какие из них наиболее связаны с рассматриваемыми характеристиками и не более.
Еще по теме Моделирование континуальности и дискретности:
- Моделирование филогенеза
- Математическое моделирование динамики популяций
- Квантовая теория — дискретные состояния — квантовые переходы
- МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭМИССИИ МЕТАНА ИЗБОЛОТ В АТМОСФЕРУ
- ЗАКОНОМЕРНОСТИ ДИНАМИКИ ЧИСЛЕННОСТИ ПОПУЛЯЦИЙ. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПОПУЛЯЦИЙ
- Лишайники
- Неодарвинизм и популяционная генетика
- Причины и скорость образования новых видов и экосистем
- Связь классической и молекулярной генетики
- Компьютерное молелирование динамики популяций
- Сущность биогеографического региона
- Ценотическая система и географическая изменчивость ценофильных видов
- Периодизация онтогенеза
- Молекулы
- МЕТОДЫ ИЗУЧЕНИЯ ГЕОХИМИЧЕСКОЙ АКТИВНОСТИ ЖИВОТНЫХ