Теория плотностных течений

Теория плотностных течений базируется на теории циркуляции В. Бьеркнеса. Она разработана В. Гелланд-Гансеном, В. Сандстремом и Н. Н. Зубовым, предложившими динамический метод вычисления морских течений.
Плотностные течения (разновидность градиентных течений) обусловлены неравномерным распределением температуры и солености воды, а, следовательно, и плотности по горизонтали.
В условиях покоя в случае совершенно однородной водной массы или когда по вертикали плотность воды с глубиной увеличивается, а по горизонтали она повсюду одинакова, поверхности равных значений гидростатического давления - изобарические - и поверхности равных значений плотности - изопикнические - параллельны друг другу. Следует отметить, что в данном случае эти поверхности параллельны также изопотенциальным поверхностям (поверхностям равных значений потенциала силы тяжести).
Море, в котором изобарические и изопикнические поверхности параллельны, называется баротропным. Море, в котором они пересекаются, называется бароклинным, именно в таком море возникают плотностные течения.
При неравномерном распределении плотностей в горизонтальном направлении изобарические и изопикнические поверхности наклонены относительно друг друга, но угол наклона между ними в природных условиях весьма небольшой. В результате пересечения изобарических и изопикнических поверхностей, проведенных через некоторые интервалы, получается система призматических трубок, называемых соленоидами. Число соленоидов характеризует динамическое состояние водных масс и свидетельствует о наличии сил, способных привести частицы воды в движение, чтобы достигнуть равновесия.
Вывод расчетной формулы плотностных течений на основе циркуляции Бьеркнеса сложен, поэтому она выводится упрощенным способом, который нагляден и приводит к одинаковому конечному результату.
Возьмем две изобарические поверхности в бароклинном море (рис. 11.6, а). Пусть одна из них р0 совпадает с поверхностью моря, а вторая р расположена на такой глубине, где плотностные течения отсутствуют (или пренебрежимо малы), и поэтому она параллельна изопотенциальной поверхности. Эта поверхность авторами динамического метода названа нулевой поверхностью.
Указанный наклон изобарической поверхности р0 свидетельствует о том, что справа плотность воды меньше, а слева больше. Очевидно, и расстояние между изобарическими по

верхностями р0 и p справа будет больше, а слева меньше, т. е.
...Предположим, что в точках м и N взяты гидрологи
ческие станции и определены значения температуры и солености воды на разных горизонтах. Проведем ряд изопотенциальных поверхностей, пересекающих изобарическую поверхность р0, и рассмотрим действие сил на частицу воды m, расположенную на этой поверхности.
Прежде всего, на частицу m действует сила тяжести g, направленная по отвесу вниз перпендикулярно изопотенциальной поверхности, и сила, обусловленная градиентом гидростатического давлениянаправленная по нормали к изобариче
ской поверхности р0 вверх. Все другие силы будем считать отсутствующими.

Рис. 11.6. Способ расчета плотностных течений



Разложим вектор силы тяжести на две составляющие: одну - вдоль поверхностии вторую - по нормали к ней
gcosp. Вторая составляющая уравновешивается градиентом гидростатического давления, а первая оказывается неуравновешенной. Частица m будет перемещаться под действием первой составляющей вектора силы тяжести вдоль изобарической поверхности р0 вдоль поверхности моря в сторону наклона уровня). Но как только начнется движениечастицы, возникнет отклоняющая сила вращения Земли, пропорциональ
ная скорости движения V и направленная в северном полушарии под углом 90° вправо к направлению движения частицы. В результате частица начнет перемещаться по равнодействующей двух сил, указанных выше, с некоторой скоростью.
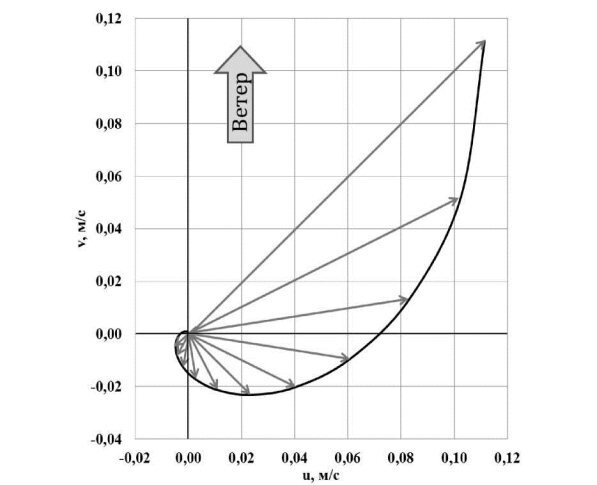
С изменением направления движения изменится и направление отклоняющей силы, что вызовет дополнительный поворот вправо равнодействующей R. Этот поворот будет продолжаться до тех пор, пока вектор течения не окажется перпендикулярным силе gsinp. В этом случае отклоняющая сила вращения Земли будет направлена в противоположную сторону и при установившемся течении будет равна силе gsinp. Возникнет динамическое равновесие (см. рис. 11.6, б), для которого сумма действующих сил должна быть равной нулю:
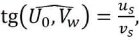(ил)

(11.2)
(11.3) (11.4)

Произведение gHM называют динамической высотой изобарической поверхности р0 (поверхности моря) в точке M относительно изобарической поверхности p (нулевой поверхности). Произведение gHN соответственно называется динамической высотой изобарической поверхности р0 относительно изобарической поверхности р в точке N. Если обозначить gHM через DM и gHN через D, то окончательно формула для вычисления плотностных течений будет иметь вид
I 1К П .              (11.5)
2io?sin:lt;p.
Интересно отметить, что оказывается безразличным, будем ли мы считать плотностное течение результатом неравномерного распределения плотности по горизонтали или само это распределение является результатом установившегося течения, с той только разницей, что в последнем случае возникает возможность рассматривать неравномерное распределение плотности как результат действия всей группы градиентных течений.
Применение динамического метода дает лучшие результаты в том случае, если: течение устойчиво и скорость его достаточно велика, глубина моря велика, так как это позволяет увереннее выбрать нулевую поверхность, гидрологические станции выполнены в короткий промежуток времени (достаточно синхронизированы во времени), гидрологические разрезы выполнены перпендикулярно существующим (или предполагаемым) течениям, район исследования расположен достаточно далеко от экватора, где горизонтальная составляющая силы Кориолиса равна нулю и, следовательно, формула плотностных течений неприменима. 

Еще по теме Теория плотностных течений:

1. Влияние морских течений на распределение температу р в водных массах. 
2. КЛИНИЧЕСКОЕ ТЕЧЕНИЕ ТЕРМИЧЕСКИХ ОЖОГОВ
3. УРОДСТВА И АНОМАЛИИ, НАРУШАЮЩИЕ ТЕЧЕНИЕ РОДОВ
4. УРОДСТВА И АНОМАЛИИ, НАРУШАЮЩИЕ ТЕЧЕНИЕ РОДОВ
5. ОСОБЕННОСТИ ТЕЧЕНИЯ РОДОВ И ПОСЛЕРОДОВОГО ПЕРИОДА У ЖИВОТНЫХ РАЗНЫХ ВИДОВ
6. Гормональная теория
7. ТЕОРИЯ, ЭВОЛЮЦИЯ И ТЕОРИЯ ЭВОЛЮЦИИ
8. 2.1. КЛЕТОЧНАЯ ТЕОРИЯ
9. Теория филэмбриогенеза
10. Мозаичная теория развития
11. 1. Какая нужна теория?
12. Теломная теория
13. Теория параллелизм